Существование решения задачи оптимального управления нелокальным уравнением баланса в пространстве знакопеременных мер (2021 г.)
Доказана теорема о существовании решения задачи оптимального управления уравнением баланса (уравнением неразрывности с источником) в пространстве знакопеременных мер с общим целевым функционалом типа Больца в классе сосредоточенных (зависящих только от времени) существенно ограниченных управлений. Результат получен для случая нелокального векторного поля и нелинейного источника при довольно слабых предположениях регулярности (в частности, без предположения компактности носителей мер-состояний). Поставленная задача обобщает известные постановки задач управления бесконечными ансамблями траекторий и охватывает ряд прикладных моделей из математической биологии и логистики. Полученные результаты могут применяться в моделировании нелокальных взаимодействий в физических (в частности, квантовых) системах, при описании динамики биологических сообществ и больших скоплений людей.
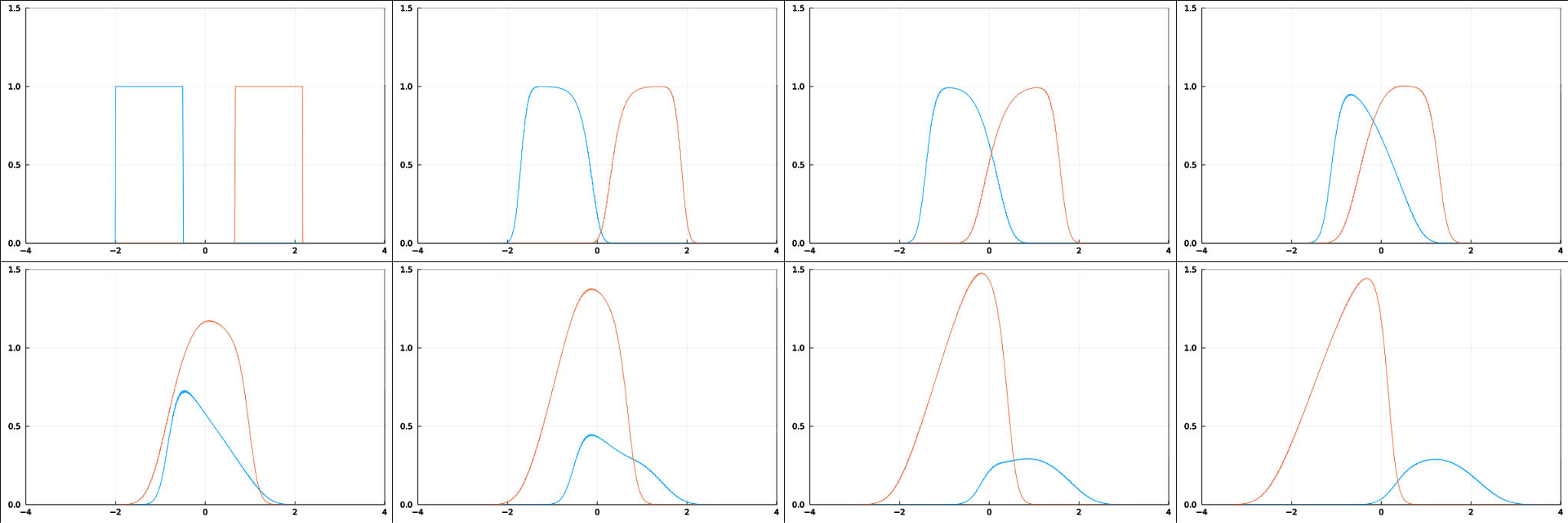
Рис. Две популяции, движущиеся навстречу друг другу, одна из которых интерферирует в другую. Каждой из популяций присуще внутреннее взаимодействие (движение замедляется с ростом плотности).
Авторы: к.ф.-м.н. Н.И. Погодаев, к.ф.-м.н. М.В. Старицын
Наиболее значимые публикации:
Погодаев Н.И., Старицын М.В. Нелокальные уравнения баланса с параметром в пространстве знакопеременных мер // Математический сборник. Том 213, № 1, 2022 https://doi.org/10.4213/sm9516 (WoS, Scopus, SJR Q1)